Question

Underground water is to be pumped by a 78% efficient 5- kW submerged pump to a pool whose free surface is 30 m above the underground water level. The diameter of the pipe is 7 cm on the intake side and 5 cm on the discharge side. Determine (a) the maximum flow rate of water (5-point) and (b) the pressure difference across the pump (5-point). Assume the elevation difference between the pump inlet and the outlet and the effect of the kinetic energy correction factors to be negligible

Answer 1

a) The maximum flowrate of the pump is approximately 13,305.22 cm³/s

b) The pressure difference across the pump is approximately 293.118 kPa

Step-by-step explanation:

The efficiency of the pump = 78%

The power of the pump = 5 -kW

The height of the pool above the underground water, h = 30 m

The diameter of the pipe on the intake side = 7 cm

The diameter of the pipe on the discharge side = 5 cm

a) The maximum flowrate of the pump is given as follows;

`P = (Q \cdot \rho \cdot g\cdot h)/(\eta_t)`

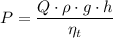
Where;

P = The power of the pump

Q = The flowrate of the pump

ρ = The density of the fluid = 997 kg/m³

h = The head of the pump = 30 m

g = The acceleration due to gravity ≈ 9.8 m/s²

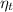`\eta_t` = The efficiency of the pump = 78%

`\therefore Q_(max) = (P \cdot \eta_t)/(\rho \cdot g\cdot h)`

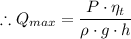
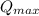`Q_(max)` = 5,000 × 0.78/(997 × 9.8 × 30) ≈ 0.0133 m³/s

The maximum flowrate of the pump
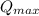`Q_(max)` ≈ 0.013305 m³/s = 13,305.22 cm³/s

b) The pressure difference across the pump, ΔP = ρ·g·h

∴ ΔP = 997 kg/m³ × 9.8 m/s² × 30 m = 293.118 kPa

The pressure difference across the pump, ΔP ≈ 293.118 kPa