Answer:
all real numbers greater than or equal to zero
Explanation:
The range of a function is defined as all possible output values it can take.
Now in our case, we have the function
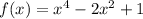
Since,
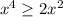
for all values of x, this tells us that the expression
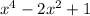
will always be greater than zero.
Therefore, we can say
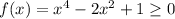
This tells us that the range of the function is all real numbers greater than or equal to zero.
Therefore, the correct answer choice is the following.
all real numbers greater than or equal to zero