Question

If 2 + 8 = 4 + 6 and 4+6 = 10 then 2 + 8 = 10Reflexive PropertyTransitive PropertySymmetric PropertySubstitution Property

Answer 1

The Transitive property states that;

`\begin{gathered} \text{If} \\ a=b\text{ and b=c} \\ \text{Then} \\ a=c \end{gathered}`

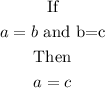
So, from the question, if a =2+8, b = 4+6 and c =10.

`\begin{gathered} \text{Then;} \\ 2+8=4+6 \\ \text{becomes,} \\ a=b \\ \text{and} \\ 4+6=10 \\ \text{becomes,} \\ b=c \\ \text{and} \\ 2+8=10 \\ \text{becomes} \\ a=c \end{gathered}`

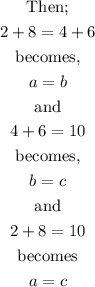
Therefore;

`\begin{gathered} If\text{ 2+8=4+6 and 4+6=10 then 2+8=10 is equivalent to the Transitive property} \\ which\text{ states that If a=b and b=c then a=c} \end{gathered}`

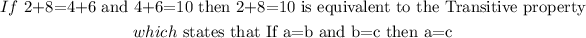
The Correct Answer is Transitive Property

The other properties in the options are;

Reflexive Property which states that any number is equal to itself for example (1=1, 2=2, a=a etc)

Symmetric Property states that if a=b then b=a.

Substitution property states that if a=b then a+c = b+c.

This other properties are incorrect and are not equivalent to the question.