Question

For a given geometric sequence, the 9th term, ag. is equal to -43/64and the 13th term, Q13, is equal to - 172. Find the value of the 17th term, a17. If applicable,write your answer as a fraction.A17=

Answer 1

Hello

To solve this question, we can simply use the formula of finding the nth term of a geometric progression.

`\begin{gathered} T_n=ar^(n-1) \\ a=\text{first term} \\ r=\text{common ratio} \end{gathered}`
`\begin{gathered} a_9=ar^8 \\ ar^8=-(49)/(64) \\ a_(13)=ar^(12)=-172 \end{gathered}`
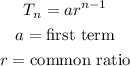
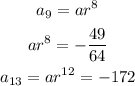
`\begin{gathered} ar^8=-(49)/(64)\ldots\text{equ 1} \\ ar^(12)=-172\ldots equ(ii) \\ \\ \text{divide equation (ii) by equation (}i) \\ (ar^(12))/(ar^8)=-(172)/(-(49)/(64)) \\ \text{divde both a} \\ (r^(12))/(r^8)=-(172)/(-(49)/(64)) \\ u\sin g\text{ division law of indicies} \\ r^(12-8)=-172*-(64)/(49) \\ r^4=(-172*-64)/(49) \\ r^4=224.65 \\ \text{take the quartic root of both side} \\ \sqrt[4]{r^4}=\sqrt[4]{224.65} \\ r=3.9 \end{gathered}`

Now that we have the value of the common ratio, we can proceed to solve for the first term which would help us find the 17th term.

we can use either of 9th term or 13th term.

Using the 13th term

`\begin{gathered} a_(13)=ar^(12)=-172_{} \\ ar^(12)=-172 \\ r=3.87 \\ a(3.9)^(12)=-172 \\ a=-(172)/(3.87^(12)) \\ a=-0.00001389 \end{gathered}`

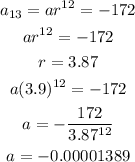
Now, let's use this to find the 17th term.

Our first term is -0.0000152 and the common ratio is 3.9

Note: Some of these values was approximated and may differ from person to person.

`\begin{gathered} a_(17)=ar^(16) \\ a_(17)=-(0.00001389)*(3.9)^(16) \\ a_(17)=-39791.185\approx-39791 \end{gathered}`

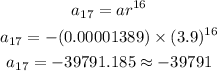
From the calculations above, the 17th term of the geometric sequence is approximately -39791