Question

Kristin and Pranav are selling cheesecakes for a school fundraiser. Customers can buy NewYorkstyle cheesecakes and apple cheesecakes. Kristin sold 12 New York style cheesecakes and8apple cheesecakes for a total of $200. Pranav sold 3 New York style cheesecakes and 1 applecheesecake for a total of $31. Write a SOE and solve it to find the cost each of one NewYorkstyle cheesecake and oneapple cheesecake?

Answer 1

EXPLANATION

Let's see the facts:

Kristin sold-------> 12 NY cheesecakes $____

8 Apple cheesecakes $____

---------------------------------------------------------------

$200

Pranav sold-------> 3 NY cheesecakes $____

1 Apple cheesecakes $____

---------------------------------------------------------------

$31

Let's call to the sale price of NY cheesecakes as x

Let's call to the sale price of apple cheesecakes as y:

We will have a system of equations as shown as follows:

(1) 12x + 8y = 200

(2) 3x + 1y = 31

Now we need to solve this system of equations:

Isolate x for 12x + 8y = 200

Subtract 8y from both sides:

12x +8y - 8y = 200 - 8y

Simplify:

12x=200-8y

Divide both sides by 12:

12x/12 = 200/12 -8y/12

Simplify:

`x=(2(-y+25))/(3)`

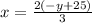
Substitute x= 2(-y+25)/3 in (2)

`\lbrack3(2(-y+25))/(3)+1y=31\rbrack`

Simplify:

`2(-y+25)\text{ +y =31}`

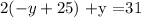
-2y +50 + y = 31

Adding -2y with y:

-y + 50 = 31

Adding -50 to both sides:

-y = 31 - 50

-y = -19

Dividing both sides by -1:

y = 19

Now substituting y=19 in the equation x=2(-y+25)/3

`x=(2(-19+25))/(3)`

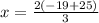
Simplifying:

`x=(2\cdot6)/(3)=(12)/(3)=4`

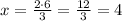
So, x=4 and y=19

We know that:

x=NY cheesecakes

y=apple cheesecakes