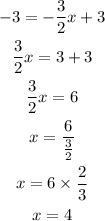Question

use the given graph of y=-3/2x+3 to solve the following equations. a) solve: 9= -3/2x+3b) solve: -3= -3/2x+3

Answer 1

The equation of the line is:

`y=-(3)/(2)x+3`

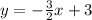
This equation is equal to "9" in part (a) and "-3" in part (b).

How do we solve the equation in part(a) and part(b) using graph?

We look at y = 9 and see at which x value it intersects with the graph.

Similarly, we look at y = -3 and see at which x value it intersects with the graph.

a)

We draw a horizontal line at y = 9. The point where it intersects the line drawn, we draw a vertical line to connect to the x-axis. So, it connects at x = -4. This is the solution. Let's check it algebraically as well.

`\begin{gathered} 9=-(3)/(2)x+3 \\ (3)/(2)x=3-9 \\ (3)/(2)x=-6 \\ x=-(6)/((3)/(2)) \\ x=-6*(2)/(3) \\ x=-4 \end{gathered}`

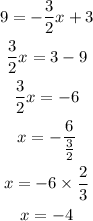
b)

We draw a horizontal line at y = -3. The point where it intersects the line drawn, we draw a vertical line to connect to the x-axis. So, it connect at x = 4. Tis is the solution. Let's check algebraically:

`\begin{gathered} -3=-(3)/(2)x+3 \\ (3)/(2)x=3+3 \\ (3)/(2)x=6 \\ x=(6)/((3)/(2)) \\ x=6*(2)/(3) \\ x=4 \end{gathered}`