Question

Suppose that sec(t) = 3/2 and that t is in quadrant IV. Find the exact value of tan(t).

Answer 1

Using the trigonometric identities

`\sec ^2(t)=\tan ^2(t)+1`

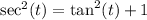
We want to find out the tan(t), then we can manipulate that formula and find tan(t) in function of sec(t).

`\tan ^2(t)=\sec ^2(t)-1`

Now we can do square roots on both sides

`\tan (t)=\pm\sqrt[]{\sec ^2(t)-1}`

We know that sec(t) = 3/2, then let's put it in our formula and simplify

`\begin{gathered} \tan (t)=\pm\sqrt[]{(3^2)/(2^2)-1} \\ \\ \tan (t)=\pm\sqrt[]{(9)/(4)-1} \\ \\ \tan (t)=\pm\sqrt[]{(9)/(4)-(4)/(4)} \\ \\ \tan (t)=\pm\sqrt[]{(5)/(4)} \end{gathered}`

We can simplify and remove 4 from the square root, and we have

`\tan (t)=\pm\frac{\sqrt[]{5}}{2}`

But which value is correct? the positive or the negative? Now we must use the information that the problem tells us, it says that t is in the quadrant IV, the tangent in quadrant IV is negative, then

`\tan (t)=-\frac{\sqrt[]{5}}{2}`