Answer:
Step-by-step explanation:
Given:
Final Amount = $1000
Time in years = 3
interest rate = 3.25% = 0.0325
To find the principal amount for the given investment, we use the formula:

Where:
P= Principal Amount
A=Final Amount
r= interest rate in decimal
t=time in years
n= the number of times interest is compounded per unit t
It is mentioned that it is compounded annually, so the value of n=1.
P=1000(1.0325) -³ is from the formula:
We plug in what we know:
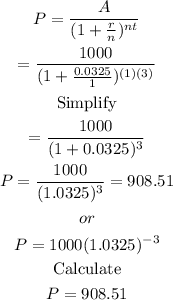
Therefore, Kyle should invest $908.51