Question

xy = 2Part AWhat is the value of z in the equation when x = 3 and y = 4? Show or explain how you gotyour answer.Part BWhat is the value of x in the equation when y = 3 and z = 125? Show or explain how you gotyour answerPart CThe student rewrote the equation as shown.z = xIs the value of x a rational number when y = 2 and z=2? Explain your reasoningPart DWrite an integer value of y and an integer value of z that makes the equation true when x = 8Show or explain how you got your answer.Your answer

Answer 1

The initial expresiion is:

`x^y=z`

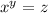
Part A: If x = 3 and y = 4 then:

`\begin{gathered} 3^4=z \\ 81=z \end{gathered}`

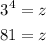
Part B: is y = 3 and z = 125 then:

`\begin{gathered} x^3=125 \\ x=\sqrt[3]{125} \\ x=5 \end{gathered}`

Part C: if he rewrite the equation as:

`\sqrt[y]{z}=x`

and y = 2 and z = 2

then x will be a rational number because z is positive and the square root of a positive number is a rational number.

Part D: If x=8 then we can give the easier value to y so let it be y = 2 then we need to find a number that the square root is equal to 8 and this number is z = 64 so:

`\sqrt[2]{64}=8`