Question

Solve for x: 2x²-2x-1=0

Answer 1

`x=(1)/(2)+\frac{\sqrt[]{3}}{2}\text{ and }x=(1)/(2)-\frac{\sqrt[]{3}}{2}`

Step-by-step explanation

Given the equation,

`2x^2-2x-1=0`

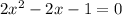
We have to solve it for x.

We can solve this using the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In our equation a = 2, b = -2 and c = -1,

`x=\frac{2\pm\sqrt[]{(-2)^2-4\cdot2\cdot(-1)}}{2\cdot2}`
`x=\frac{2\pm\sqrt[]{4+8}}{4}`
`x=\frac{2\pm\sqrt[]{12}}{4}=\frac{2\pm\sqrt[]{4\cdot3}}{4}=\frac{2\pm2\sqrt[]{3}}{4}`

Distribute the denominator into the addition/subtraction,

`x=(2)/(4)\pm\frac{2\sqrt[]{3}}{4}=(1)/(2)\pm\frac{\sqrt[]{3}}{2}`

The values of x that are solution to this equation are,

`x=(1)/(2)+\frac{\sqrt[]{3}}{2}\text{ and }x=(1)/(2)-\frac{\sqrt[]{3}}{2}`