Question

Use the central limit theorem to find the mean and standard error of the mean of the indicated sampling distribution. Then sketch a graph of the sampling distributionThe per capita consumption of red meat by people in a country in a recent year was normally distributed, with a mean of 108 pounds and a standard deviation of 37.9pounds. Random samples of size 17 are drawn from this population and the mean of each sample is determined.u(x) =. (Round to three decimal places as needed)Sketch a graph of the sampling distribution.

Answer 1

We have a population normally distributed with a mean of 108 pounds and a std deviation of 37.9 pounds.

The sample size is 17.

The sample mean is expected to be equal to the population mean, so it will be 108 pounds.

The standard error for this sample size can be calculated as:

`\sigma_s=\frac{\sigma}{\sqrt[]{n}}=\frac{37.9}{\sqrt[]{17}}\approx9.192`

Then, we have a sampling mean of 108 and a std. error of 9.192.

Most of the data (95%) should be within 2 std. error from the mean. This is between 90 and 126:

`\begin{gathered} 108-2\cdot9.192\approx90 \\ 108+2\cdot9.192\approx126 \end{gathered}`

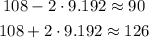
Then, graph number C shows this condition: most of the data is within 90 and 126, with a mean of 108.

Answer:

μs = 108

σs = 9.192

Graph C is representing the sampling distribution.