Kobe made 25 shots
Step-by-step explanation
Step 1
Let x represents the number of shot made
Let y represents the number of shot loses
total points = 0
Hence,
For each shot made, the player earns three points. For each shot missed, the player loses five points
total points= 3x-5y
so
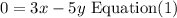
Also, the total shots is 40, so
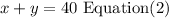
Step 2
write and solve the system
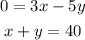
isolate x in equation (2) and replace in equation(1)

Step 3
replace the value of y in equation (3) to find x
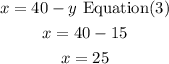
so,Kobie made 25 shots