Question

In the rectangle below A equals 4X plus 7V equals 5X +1 and M angle ECD equal 30°

Answer 1

We are given that the distance from a vertex to the center of a rectangle is the same for every vertex. Therefore, we have:

`\bar{AE}=\bar{BE}`

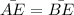
Since the segments are given as algebraic expressions we may replace them in the previous relationship:

`4x+7=5x+1`

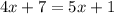
Now we solve for "x" first by subtracting "5x" from both sides:

`\begin{gathered} 4x+7-5x=5x+1-5x \\ -x+7=1 \end{gathered}`

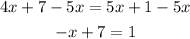
Now we subtract 7 from both sides:

`\begin{gathered} -x+7-7=1-7 \\ -x=-6 \end{gathered}`

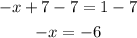
Now we multiply both sides by -1:

`x=6`

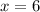
Therefore, x = 6. Since we are asked the length of AC, we have:

`\bar{AC}=\bar{AE}+\bar{EC}`

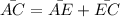
we can use the fact that the diagonal AC is bisected at the interception with diagonal BD, therefore:

`\bar{AC}=2\bar{AE}`

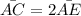
Now we substitute the algebraic expression for segment AE:

`\bar{AC}=2(4x+7)`

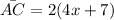
Now we substitute the value of "x":

`\bar{AC}=2(4(6)+7)`

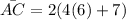
Solving the operations:

`\bar{AC}=62`

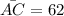
Therefore, the length of AC is 62

We are also asked to determine the value of the angle EBC given that angle ECD is 30 degrees. We will use the fact that the angles are the vertex of a rectangle are right angles, therefore:

`m\angle ECD+m\angle ECB=90`

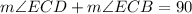
Solving for angle ECB we get:

`m\angle ECB=90-m\angle ECD`

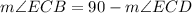
Now we substitute the value of angle ECD:

`m\angle ECB=90-30=60`

Since segments EB and EC are equal, this means that triangle EBC is an isosceles triangle. In an isosceles triangle the base angles are equal, therefore:

`m\angle ECB=m\angle EBC=60`

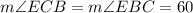
Therefore, the measure of angle EBC is 60 degrees.