Question

A sculpture is 4.00 m tall and has its center of gravity located 1.90 m above the center of its base. The base is a square with a side of 1.50 m. To what angle θ can the sculpture be tipped before it falls over?

Answer 1

Given,

The height of the sculpture, h=4.00 m

x=1.90 m

y=1.50 m

The sculpture will tip over when the CG crosses the point of contact of the sculpture and the floor. Thus θ will have the maximum value when the CG is exactly above the point of contact.

When the point CG is directly above the point of contact, CG, point of contact (P) and the center of the base (C) forms a right angle triangle as shown:

From the diagram,

`\begin{gathered} \theta=\tan ^(-1)(((y)/(2))/(x))_{} \\ =\text{tan}^(-1)((y)/(2x)) \end{gathered}`

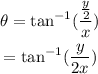
On substituting the known values,

`\begin{gathered} \theta=\tan ^(-1)((1.50)/(2*1.90)) \\ =21.5\degree^{} \end{gathered}`

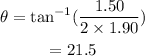
Thus the sculpture can be tipped to an angle of 21.5° before it falls.