Question

Check for parallel lines and right angles by using the slope formula

Answer 1

In this stage of the problem, we need to figure out how the slopes of each segment are related to each other. Well'll begin by find the slope for each segment: AB, BC, CD, and DA.

Slope of AB

We are given the points

`\begin{gathered} A(4,-6) \\ B(-1,-6) \end{gathered}`

To find the slope between the two points, we'll use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

From our points, we have:

`m=(-6-(-6))/(-1-4)=(0)/(-5)=0`

The slope of AB is 0.

Slope of BC

We have the points for B and C:

`\begin{gathered} B(-1,-6) \\ C(3,-3) \end{gathered}`

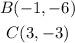
Using the slope formula again, we get

`m=(-3-(-6))/(3-(-1))=(3)/(4)`

The slope of BC is 3/4.

Slope of CD

The points for C and D are:

`\begin{gathered} C(3,-3) \\ D(8,-3) \end{gathered}`

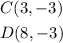
From the slope formula, we get:

`m=(-3-(-3))/(8-3)=(0)/(5)=0`

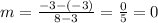
The slope of CD is 0.

Slope of DA

Using points D and A:

`\begin{gathered} D(8,-3) \\ A(4,-6) \end{gathered}`

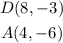
We get:

`m=(-6-(-3))/(4-8)=(-3)/(-4)=(3)/(4)`

The slope of DA is 3/4.

Comparing the slopes of all the lines

Now that we have the slope for each line, we want to determine if there are any parallel or perpendicular lines represented.

Parallel lines have the same slope, and perpendicular lines have slopes that are opposite reciprocals (for example 1/2 and -2).

Here's what we found:

- AB has a slope of 0

- BC has a slope of 3/4

- CD has a slope of 0

- DA has a slope of 3/4

Since AB and CD have the same slope, they are parallel to each other.

Since BC and DA have the same slope, they are parallel to each other.

None of the segments provided are perpendicular.