Question

Find all y-intercepts and x-intercepts of the graph of the function.If there is more than one answer, separate them with commas. Click on "None" if applicable.

Answer 1

Given

`y=f(x)=2x^3+8x^2-2x-8`

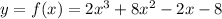
Find

x-intercept and y-intercept

Step-by-step explanation

To find the y intercept, put x=0 in the above equation

`\begin{gathered} y=f(x)=2(0)^3+8(0)^2-2(0)-8 \\ y=-8 \end{gathered}`

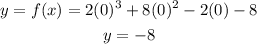
Now Finding x intercept

`\begin{gathered} f(x)=2x^3+8x^2-2x-8 \\ f(1)=2(1)^3+8(1)^2-2(1)-8 \\ f(1)=0 \end{gathered}`

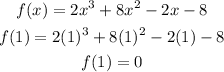
Therefore x-1 is a factor of the above equation

Divide f(x) with x-1, we get

`\begin{gathered} (2x^3+8x^2-2x-8)/(x-1) \\ =2x^2+10x+8 \end{gathered}`

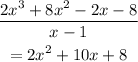
Now finding the factors of this quadratic equation

`\begin{gathered} 2x^2+10x+8=0 \\ 2x^2+8x+2x+8=0 \\ 2x(x+4)+2(x+4)=0 \\ (x+4)(2x+2)=0 \\ (x+4)(x+1)=0 \end{gathered}`

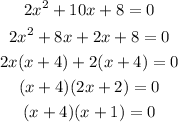
Therefore,

x=-4,-1

Final Answer

x-intercepts = 1,-1,-4

y-intercepts= -8