In a right triangle, the tangent of an angle is the length of the opposite side divided by the length of the adjacent side. In our triangle, 7 is the adjacent side to 30º, and x is the opposite side.
From this, we have the following relation
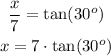
The tangent of 30º ise a known value
![\tan (30^o)=\frac{1}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/5nqowwqkgm42jiv9d3ysg89z2xcawk2frz.png)
Solving for x, we have
![\begin{gathered} x=\frac{7}{\sqrt[]{3}} \\ x=4.04145188433\ldots \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/toxsbpjra7u8chwuyb7uv1k112sd91vr2d.png)