Question

1. An observer 80 ft above the surface of the water measures an angle of depression of 0.7o to a distant ship. How many miles is the ship from the base of the lighthouse? (5280 ft = 1 mile)

Commercial airliners fly at an altitude of about 10 km. They start descending toward the airport when they are far away, so that they will not have to dive at a steep angle.


2 a) If the pilot wants the plane's path to make an angle of 3o with the ground, at what horizontal distance must the plane start descending?


b) If the pilot starts descending a ground distance of 300 km from the airport, what angle will the plane's path make with the horizontal?


3. A submarine at the surface of the ocean makes an emergency dive, making an angle of 21o with the surface. If it travels for 300 m along a downward path, how deep will it be?

Answer 1

1. The distance of the ship from the base of the lighthouse is approximately 1.24 miles

2. a)The horizontal distance the plane must start descending is approximately 190.81 km

b) The angle the plane's path will make with the horizontal is approximately 18.835°

3. The depth of the submarine is approximately 107.51 m

Explanation:

The

1. From the question, we have;

The height of the observer above the water = 80 ft.

The angle of depression of the ship from the observer, θ = 0.7°

Let the position of the observer be 'O', let the location of the ship be 'S', let the point directly above the ship at the level of the observer be 'H', we have;

`tan(\theta) = (Opposite \ leg \ length)/(Adjacent \ leg \ length) = (HS)/(OH)`

`The \ horizontal \ distance \ of \ the \ ship, OH = (HS)/(tan(\theta) )`

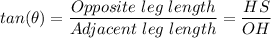
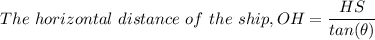
HS = The height of the observer = 80 ft.

Therefore, we get;

`The \ horizontal \ distance \ of \ the \ ship, OH = (80 \, ft.)/(tan(0.7^(\circ)) ) \approx 6,547.763 \ ft.`

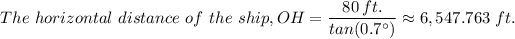
The distance of the ship from the base of the lighthouse ≈ 6,547.763 ft. ≈ 1.24 miles

2. The elevation of the plane, h = 10 km

The angle of the planes path with the ground, θ = 3°

Similar to question (1) above, the horizontal distance the plane must start descending, d = t/(tan(θ))

∴ d = 10 km/(tan(3°)) ≈ 190.81 km

The horizontal distance the plane must start descending, d = 190.81 km

b) If the pilot start descending 300 km from the airport, the angle the plane's path will make with the horizontal, θ, will be given as follows;

From trigonometry, we have;

`tan(\theta) = (Opposite \ leg \ length)/(Adjacent \ leg \ length)`

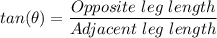
Where the opposite leg length = The elevation of the plane = 10 km

The adjacent leg length = The horizontal distance from the airport = 300 km

`\therefore tan(\theta) = (10 \, km)/(300 \, km) = (1)/(3)`

`\theta = arctan\left((1)/(3) \right ) \approx 18.835^(\circ)`

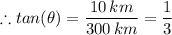
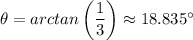
The angle the plane's path will make with the horizontal, θ ≈ 18.835°

3. The angle at which the submarine makes the deep dive, θ = 21°

The distance the submarine travels along the inclined downward path, R = 300 m

By trigonometric ratios, we have;

The depth, of the submarine, 'd' is given as follows;

`si(\theta)= (Opposite \ leg \ length)/(Hypotenuse \ length) = (d)/(R)`

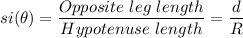
∴ d = R × sin(θ)

d = 300 m × sin(21°) ≈ 107.51 m

The depth of the submarine ≈ 107.51 m