Question

Which equation represents a line that is parallel to y = -4x + 3 and passes through the point (-3, 2)?a. y = -4X – 10b. y = -4x + 2c. y = -4x + 5d. y = 1/4x - 7/2e. y = 1/4x + 11/4

Answer 1

when 2 lines are parallels , have the same slope

the slope of

`y=-4x+3`

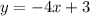
is -4 because is the coefficient of x

so I write the general equation of the line and replace the slope

`\begin{gathered} y=mx+b \\ \\ y=-4x+b \end{gathered}`

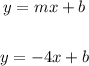
to find b, I replace the point (-3,2) since this must be fulfilled

so

`2=-4(-3)+b`

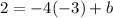
and solve b

`\begin{gathered} 2=12+b \\ b=2-12 \\ b=-10 \end{gathered}`

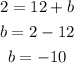
the equation of the parellel line is

`y=-4x-10`

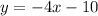
so the right option is A