Step-by-step explanation
In the question, we are given that the individual should be able to withdraw $45,000 each year for 20 years through his account that earns 10% interest.
To find the amount he would need at in the account at the beginning, we will use the Payout Annuity formula below.
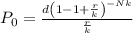
Where
P is the balance in the account at the beginning (starting amount, or principal).
d is the regular withdrawal (the amount you take out each year, each month, etc.)
r is the annual interest rate (in decimal form. Example: 5% = 0.05)
k is the number of compounding periods in one year.
N is the number of years we plan to take withdrawals

Answer: $383110.36738