We have the function:
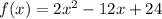
to find its vertex and axis of symmetry we need to write it in standard form. To do this we need to complete the squared, let's do that:
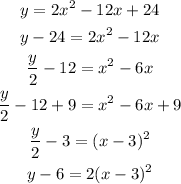
Now, we recognize the last equation as the equation of a vertical parabola of the form:
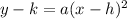
We know that this parabola has vertex in the point (h,k). Then, comparing both equations, we conclude that the vertex is the point (3,6).
We also know that the axis of symmetry on this kind of equations are given by the equation x=h. In this case this means that the axis of symmetry is:
