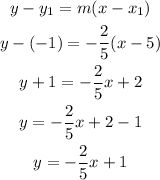Question

Write an equation that passes through (5,-1) and is perpendicular to y=5/2x-5

Answer 1

`y=-(2)/(5)x+1`

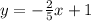
Explanation:

The equation of a line is represented by the following equation:

`\begin{gathered} y=mx+b \\ \text{where,} \\ m=\text{ slope} \\ b=y-\text{intercept} \end{gathered}`

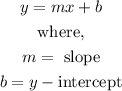
If the given line is perpendicular to the one we want to find, the slope of the missing line would be the negative reciprocal of the given slope:

`\begin{gathered} m=-((2)/(5)) \\ m=-(2)/(5) \end{gathered}`

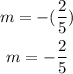
Use the slope-point form of the line equation to determine the equation in slope-intercept form:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-1)=-(2)/(5)(x-5) \\ y+1=-(2)/(5)x+2 \\ y=-(2)/(5)x+2-1 \\ y=-(2)/(5)x+1 \end{gathered}`