Question

Question 9 of 17, Step 1 of 28/21Correct2Consider the following equation,4x - 2y = -12Step 1 of 2: Determine the missing coordinate in the ordered pair (-1, ?) so that it will satisfy thegiven equationAnswerHow to enter your answer (opens in new window)HB KeypadKeyboard Shortcuts(-1,

Answer 1

- The question gives us the following equation

`4x-2y=-12`

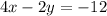
Question 1:

- We are asked to find the missing coordinate in the ordered pair ( - 1, ?).

- From the coordinate, we can see that the y-value of the ordered pair is what is missing.

- If the ordered pair satisfies the equation, it means that for the value of x = -1. there must be a corresponding y-value.

- In order to find this y-value, we simply substitute x = - 1 into the equation given to us. After this, we solve for y.

- The value of y that we get from the equation gives the corresponding value of x = 1 in the ordered pair (-1, ?)

- Now, let us solve for y as follows:

`\begin{gathered} 4x-2y=-12 \\ \text{put }x=-1 \\ 4(-1)-2y=-12 \\ -4-2y=-12 \\ \text{Add 4 to both sides} \\ -2y=-12+4 \\ -2y=-8 \\ \text{Divide both sides by -2} \\ y=-(8)/(-2) \\ \\ \therefore y=4 \end{gathered}`

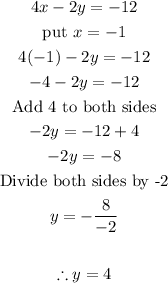
- Thus, the ordered pair is (-1, 4)

Question 2:

- We are given the following ordered pair (?, 10).

- We simply follow the same process. We take the y-value, 10, and substitute it into the equation to find the x-value that would replace the "?" sign

- Thus, we solve as follows:

`\begin{gathered} 4x-2y=-12 \\ \text{Put }y=10 \\ 4x-2(10)=-12 \\ 4x-20=-12 \\ \text{Add 20 to both sides} \\ 4x=-12+20 \\ 4x=8 \\ Divide\text{ both sides by 4} \\ x=2 \end{gathered}`

- Thus, x = 2, when y = 10. The answer is (2, 10)

Final Answer

- Question 1: (-1, 4)

- Question 2: (2, 10)