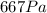Question

a quantity of gas in a piston cylinder has a volume of 0.500 m^3 to the power and a pressure of 200 Pa. the Piston compresses the gas to 0.150 m^3 in an isothermal ( constant temperature) process what is the final pressure of the gas

Answer 1

According to Boyle's Law, an ideal gas at a constant temperature will satisfy the following relation between the initial and final conditions of pressure and volume:

`P_1V_1=P_2V_2`

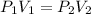
Isolate P_2 from the equation:

`P_2=\frac{_{}P_1V_1_{}_{}}{V_2}`

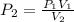
Substitute the values for the initial pressure as well as for the two volumes to find the value of the final pressure of the gas:

`\begin{gathered} P_2=((200Pa)(0.500m^3))/((0.150m^3)) \\ =667Pa \end{gathered}`

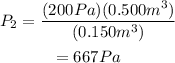
Therefore, the final pressure of the gas is:

`667Pa`