The U.S RDA for protein is 46g for girl
If a piece of fried chicken contains 23g
To find the pieces of chicken she is to eat to satisfy the U.S RDA requirement,
The number of pieces of chicken is
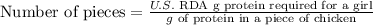
The number of pieces of chicken is
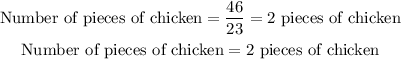
Hence, the right option is B