Question

Calculate the sum of the first 8 terms of the arithmetic sequence in which a8=-1 and the common difference is d=-8

Answer 1

In the arithmetic sequence, the nth term is

`a_n=a+(n-1)d`

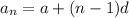
a is the first term

d is the common difference

n is the position of the number

Since a(8) = -1

Then n = 8

Since the common difference is -8, then

d = -8

Substitute them in the rule to find the first term a

`\begin{gathered} -1=a+(8-1)(-8) \\ -1=a+(7)(-8) \\ -1=a-56 \end{gathered}`

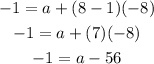
Add 56 to each side

`\begin{gathered} -1+56=a-56+56 \\ 55=a \end{gathered}`

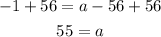
The first term is 55

The rule of the sum of the nth term is

`S_n=(n)/(2)\lbrack a+l\rbrack`

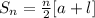
l is the last term

Since we need the sum of 8 terms, then

a = 55

l = a(8) = -1

n = 8

`\begin{gathered} S_8=(8)/(2)\lbrack55+(-1)\rbrack \\ S_8=4\lbrack54\rbrack \\ S_8=216 \end{gathered}`

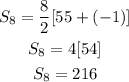
The sum of the first 8 terms is 216

The answer is A