Question

An airplane can travel 370mph in still air. If it travels 2737 miles with the wind in the same length of time it travels 2443 miles against the wind, what is the speed of the wind?

Answer 1

Given:

An airplane can travel 370 mph in still air

If it travels 2737 miles with the wind in the same direction of the speed

Let, the speed of the wind = x

speed = distance over the time

`x+370=(2737)/(t)\rightarrow(1)`

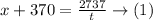
And it travels 2443 miles at the same time against the wind

`-x+370=(2443)/(t)\rightarrow(2)`

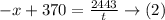
Solve the equations to find x, and t

Add the equations:

`\begin{gathered} 370\cdot2=(1)/(t)(2737+2443) \\ t=(2737+2443)/(2\cdot370)=7 \end{gathered}`

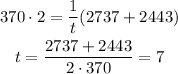
Substitute with (t) into equation (1) to find (x)

`\begin{gathered} x+370=(2737)/(7) \\ x+370=391 \\ x=391-370 \\ x=21 \end{gathered}`

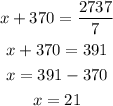
So, the answer will be:

The speed of the wind = 21 mph