Finding the solution algebraically
To answer this inequality, we can follow the next steps:
1. Multiply by 7 both sides of the inequality:
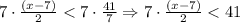
2. Multiply by 2 both sides of the inequality:
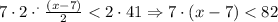
3. Apply the distributive property at the left side of the inequality:

4. Add 49 to both sides of the inequality:
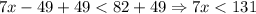
5. Finally, divide both sides of the inequality by 7:
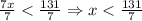
We can graph this inequality in the number line as follows:
Notice the parenthesis indicating that the solution is the number below 131/7 (but not equal to 131/7). In interval notation the solution is:
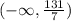
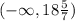
Or, approximately:

The number 131/7 in decimal is equivalent to 18.7142857143, so the graph of the solution is given by graph A (we can see that there are seven divisions between 18 and 19; since we have that the shaded division is in the 5th division, then, we have 5/7 = 0.714285714286, that is, the decimal part of the above number).
We can express the number 131/7 as a mixed number as follows:
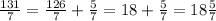
Again, notice also the symbol for the left part of the interval notation is a parenthesis since the interval is open at the point 131/7 = 18 + 5/7.
Finding the solution graphically
To find the solution graphically, we can represent the inequality as two lines as follows:

Then, if we graph the first line, we can find the x- and the y-intercepts to find two points to graph the line. We have that the x- and the y-intercepts are:
The x-intercept is (that is, when y = 0):
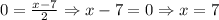
Then, the x-intercept is (7, 0), and the y-intercept (the point on the graph when x = 0) is:
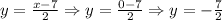
Then, the y-intercept is (0, -7/2).
The other line is given by:
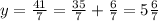
With this information, we can graph both lines:
And we can see that the point where the two lines coincide is:

Then, the values for x of the line (x-7)/2 [that is, the values of y = (x-7)/2] that are less than y = 41/7, represented as:
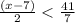
Are those values of x less than 131/7, or the solution is also (we express the solution as a fraction or a mixed number as follows) (the same solution):
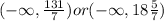
In summary, we have that the solution to the inequality is:
As an inequality:
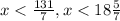
In interval notation:
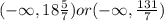
And the representation of the solution on the number line is (option A):