Question

The figure shows a walkway around a swimming pool. The width of the walkway is 4 1/2 ft all the way aroundWhat is the area of the walkwayA 605 ft2B 1,251 ft2C 2'682 ft2B 3,675 ft2LAST QUESTION OF THE DAY HELP ME OUT!!!

Answer 1

First, we have to transform the mixed number into a fraction.

`4(1)/(2)=(4\cdot2+1)/(2)=(8+1)/(2)=(9)/(2)`

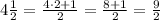
The width of the walkway is 9/2 feet.

Notice the length of the small rectangle is 30 feet. We have to sum 9/2 twice to 30 because the width of the walkway is on both sides like the image below shows.

The sum for the length of the walkway is

`(9)/(2)+30+(9)/(2)=30+(9+9)/(2)=30+(18)/(2)=30+9=39`

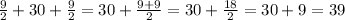
The length of the walkway is 39 feet.

The sum for the width is

`(9)/(2)+100+(9)/(2)=100+(9+9)/(2)=100+(18)/(2)=100+9=109`

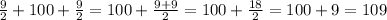
The width of the walkway is 109 feet.

Now, to find the area we multiply the length and the width.

`A=39\cdot109=4,251ft^2`

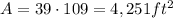
However, we have to subtract the area of the smaller rectangle to find the actual area of the walkway.

`A_(small)=100\cdot30=3000ft^2`

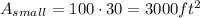
Then,

`A_(walk)=A-A_(small)=4,251-3000=1,251ft^2`

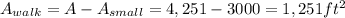
Therefore, the answer is B.