Question

What is an equation of the line that passes through the point (6,3)(6,3) and is parallel to the line x+3y=24x+3y=24?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about lines and properties of parallel lines.

We want to determine the equation of a line that passes through the point (6, 3) and is parallel to the line x + 3y = 24.

First, we'll rewrite the equation of this line, that was given in general form, into slope-intercept form:

For this, simply solve the equation for y

Subtract x on both sides of the equation

`3y=24-x`

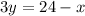
Divide both sides of the equation by a factor of 3

`y=-(1)/(3)x+8`

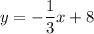
We need this because in this form it is easier to find the slope of this line:

`y=mx+b`

So we find that

`m=-(1)/(3)`

Is the slope of this line.

A line that is parallel to this has the same slope, such that we can use the following equation to find the answer:

`y=y_0+m(x-x_0)`

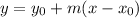
Whereas (x0, y0) is the point the line passes through and m is the slope.

Plugging (x0, y0) = (6, 3) and m = -1/3 as we found, we get

`y=3-(1)/(3)\cdot(x-6)`

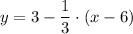
Multiply both sides of the equation by 3

`\begin{gathered} 3y=9-(x-6) \\ \\ 3y=9-x+6 \\ \\ 3y=15-x \\ \end{gathered}`

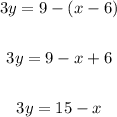
Add x on both sides of the equation

`x+3y=15`

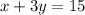
This is the equation of the line passing through the desired point and is parallel to the line we had.