Question

Explain how you find the Least Common Denominator of x^2+5x+4 and x^2-16

Answer 1

Find the least common denominator (L.C.D ) of the expressions below

`(x^2+5x+4),(x^2-16)`

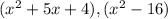
Concept:

We will factorize each of the expressions and then find the least common denominator of both of them

Step 1:

Factorize

`x^2+5x+4`

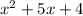
To do this, we will have to look for two numbers that can be multiplied each other to give +4 and the same two numbers will add up to give +5

By try and error, we will have

`\begin{gathered} +2*+2=+4,+2+2=+4\text{ (wrong )} \\ +1*+4=+4,+1++4=+5(right) \end{gathered}`

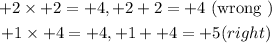
From the above illustration, the two numbers to be used are +1 and +4

Replace the 5x with +x and +4x in the expression below

`\begin{gathered} x^2+5x+4 \\ =x^2+x+4x+4 \\ =(x^2+x)+(4x+4) \\ =x(x++1)+4(x+1) \\ =(x+1)(x+4)_{} \end{gathered}`

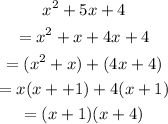
Step 2:

Factorize the expression below using the difference of two squares

`x^2-16`

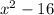
The difference of the two squares involve

`a^2-b^2=(a-b)(a+b)`

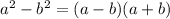
By applying the principle above, we will have

`\begin{gathered} x^2-16=x^2-4^2 \\ =(x-4)(x+4) \end{gathered}`

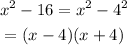
Note:

The Least Common Denominator will have everything from both - but not duplicated.

Therefore,

The least common denominator of (x² +5x +4 and (x² -16) is = (x + 4)(x - 4)(x -1 )