Question

How do I find the lateral area of the pyramid rounded to the nearest whole number??

Answer 1

2362 square meters.

Explanation:

Given:

Side = a = 30

Height = h = 36.4

s = slant length

We can calculate the lateral area of the pyramid as follows:

`\begin{gathered} A_L=4\cdot\mleft((1)/(2)\cdot\: a\cdot\: l\mright) \\ A_L=2\cdot a\cdot l \end{gathered}`

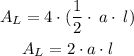
We can determine the inclined length by means of the Pythagorean theorem, assuming that one side is a/2 and the other side is the height.

Therefore:

`\begin{gathered} A_L=2\cdot a\cdot\sqrt{\left((a)/(2)\right)^2+h^2} \\ A_L=2\cdot a\cdot\sqrt[]{(a)/(4)+h^2} \end{gathered}`

We replacing:

`\begin{gathered} A_L=2\cdot30\cdot\sqrt{(30^2)/(4)+\left(36.4\right)^2} \\ A_L=2362.17\cong2362m^2 \end{gathered}`

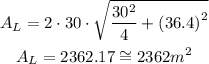
The area of the pyramid is equal to 2362 square meters.