C
1) Since the diameter of a circle is at (3,-7) and (5,7) then we can find the radius this way.
(x-h) +(y-k)² = r²
2) The Center is at the midpoint of the Diameter, then let's find out the midpoint of the line whose endpoints are (3,-7) and (5,7)
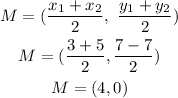
2.2) Now, we need to find out the radius. Let's pick one of those points (5,7) and the Midpoint (4,0) and find out the distance:
![\begin{gathered} d=\sqrt[]{(x_1-x_2)^2+(y_1-y_2)^2}_{} \\ d=\sqrt[]{(5-4)^2+(7-0)^2} \\ d=\sqrt[]{50} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fgxtd7lmexvxc5rh9utu0hvta2cxxxx108.png)
This distance between one of those endpoints and this midpoint is the radius.
3) Finally, let's plug into the equation of the Circle the following:
![\begin{gathered} (x-4)^2+y^2=(\sqrt[]{50})^2 \\ (x-4)^2+y^2=50 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vai9wzr5l42kmwi5mgvnsqjnhwz1d5ysyd.png)
Hence, the answer is C