Question

A scientist has two solutions, which has labeled solution A abd solution B . each salt contain she knowns that solution A is 60% salt and solution B is 85% salt. she want to obtain 180 ounces of a mixture that is 70% salt how many ounces of each solution should she use

Answer 1

To do this, you can first express the percentages as decimals, like this

`\begin{gathered} 60\text{ \%}=(60)/(100)=0.6 \\ 85\text{ \%}=(85)/(100)=0.85 \\ 70\text{ \%}=(70)/(100)=0.7 \end{gathered}`

Later, you can take

x = number of ounces of solution A

y = number of ounces of solution B

And build the following system of linear equations

`\begin{gathered} \mleft\{\begin{aligned}x+y=180 \\ 0.6x+0.85y=0.7\cdot180\end{aligned}\mright. \\ \mleft\{\begin{aligned}x+y=180 \\ 0.6x+0.85y=126\end{aligned}\mright. \end{gathered}`

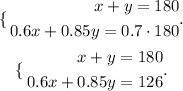
To solve it you can use the substitution method, for example.

Solve for x from the first equation and substitute this value in the second equation

`\begin{gathered} x+y=180 \\ \text{ Subtract y from both sides of the equation} \\ x+y-y=180-y \\ x=180-y \end{gathered}`

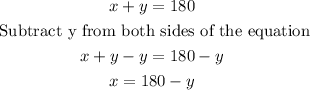
Now substituting in the second equation

`\begin{gathered} 0.6(180-y)+0.85y=126 \\ 108-0.6y+0.85y=126 \\ 108+0.25y=126 \\ \text{ Subtract 108 from both sides of the equation} \\ 108+0.25y-108=126-108 \\ 0.25y=18 \\ \text{ Divide both sides of the equation by }0.25 \\ (0.25y)/(0.25)=(18)/(0.25) \\ y=72 \end{gathered}`

Now plug the value of y into the first equation

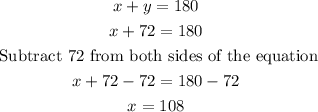
`\begin{gathered} x+y=180 \\ x+72=180 \\ \text{ Subtract 72 from both sides of the equation} \\ x+72-72=180-72 \\ x=108 \end{gathered}`

So,

`\mleft\{\begin{aligned}x=108 \\ y=72\end{aligned}\mright.`

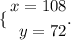
Therefore, the scientist should use 108 ounces of solution A and 72 ounces of solution B.