Question

Really need help answering this, having trouble solvingIt’s from my ACT prep guide online

Answer 1

When an angle is drawn in standard position its vertex is located at the point (0,0) in the grid and its initial side has to be located along the positive x-axis. So basically the initial side of angle A is any segment along the positive x-axis and its terminal side is the segment between (0,0) and (10,-4). Here is important to recall an important property of angles in standard position.

If its terminal side of angle A has a length of 1 unit then its extreme is given by the point (cosA,sinA). So if we find a 1 unit segment that is part of the old terminal side of A we can brand it as the new terminal side (the measure of the angle doesn't change, only the length of the side) and use its end to find the cosine of A. With the cosine of A we can find sec(A).

So first of all let's find our new terminal side. This has to be a segment inside the original terminal side that starts at point (0,0) so in order to find its end we just need to multiply (10,-4) by a positive number:

`a\cdot(10,-4)=(10a,-4a)`

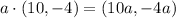
The length of this side is given by the square root of the sum of the squares of its coordinates and it has to be equal to 1:

`\begin{gathered} \sqrt[]{(10a)^2+(-4a)^2}=1 \\ \sqrt[]{100a^2+16a^2}=\sqrt[]{116a^2}=1 \end{gathered}`

If we square both sides of this equation we get:

`\begin{gathered} (\sqrt[]{116a^2})^2=1^2 \\ 116a^2=1 \end{gathered}`

Then we divide both sides by 116 and then we apply a square root:

`\begin{gathered} 116a^2=(1)/(116) \\ a^2=(1)/(116) \\ √(a^2)=\sqrt{(1)/(116)} \\ a=\frac{1}{\sqrt[]{116}} \end{gathered}`

So the new terminal side is the segment between (0,0) and:

`(\frac{10}{\sqrt[]{116}},-\frac{4}{\sqrt[]{116}})`

Which means that the cosine of A is:

`\cos A=\frac{10}{\sqrt[]{116}}`

And the secant is defined as 1 divided by the cosine so we have:

`\sec A=(1)/(\cos A)=\frac{1}{\frac{10}{\sqrt[]{116}}}=\frac{\sqrt[]{116}}{10}`

Then the answer is:

`\sec A=\frac{\sqrt[]{116}}{10}`