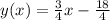Question

Find the equation of line from the given graph:

Answer 1

`y(x)=(3)/(4)x-(18)/(4)`

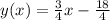
Step-by-step explanation: We need to write the equation of the line which has the general form:

`y(x)=mx+b`

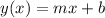
Where:

`\begin{gathered} m=(\Delta y)/(\Delta x) \\ b=y-\text{intercept} \end{gathered}`

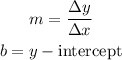
These two parameters are found as follows:

Slope:

`\begin{gathered} P_1(-2,-6) \\ P_2(2,-3) \\ \therefore\rightarrow \\ m=(\Delta y)/(\Delta x)=(-6-(-3))/(-2-2)=(-3)/(-4)=(3)/(4) \end{gathered}`

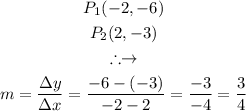
y-intercept:

From the graph, it is the point where the line intersects the y-axis, therefore it is:

`\begin{gathered} y(-2)=-6=(3)/(4)(-2)+b \\ \therefore\rightarrow \\ b=-6+(6)/(4)=(-24+6)/(4)=(-18)/(4)=-4.5 \end{gathered}`

And the graph agrees with it:

Equation of line is:

`y(x)=(3)/(4)x-(18)/(4)`