Right triangles are those triangle that have an angle whose measure is 90 degrees (which is also called "Right angle").
The Pythagorean Theorem states that:
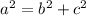
Where "a" is the hypotenuse (the longest side), and "b" and "c" are the legs of the Right triangle.
In this case, you can determine if Jerry can create a Right triangle with the side lengths given in the exercise, as following:
1. Identify the longest side of the triangle (the hypotenuse):
![a=7\operatorname{mm}]()
2. Identify the legs:
![\begin{gathered} b=3\operatorname{mm} \\ c=5\operatorname{mm} \end{gathered}]()
3. Check if it is a Right triangle using the Pythagorean Theorem:
![\begin{gathered} (7\operatorname{mm})^2=(3\operatorname{mm})^2+(5\operatorname{mm})^2 \\ 49mm^2\\e34\operatorname{mm}^2 \end{gathered}]()
As you can observe, Jerry can't create a Right triangle using those side lengths.
The answer is: Second option.