SOLUTION
Given the question in the question tab, the following are the solution steps to solve the question
STEP 1: Define a countably infinite set
A set is countably infinite if its elements can be put in one-to-one correspondence with the set of natural numbers. In other words, one can count off all elements in the set in such a way that, even though the counting will take forever, you will get to any particular element in a finite amount of time.
STEP 2: Write the given set

This set is read as a set of values 2q such that q is an element of positive rational numbers
STEP 3: Show the proof
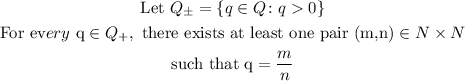
Therefore, we can find an injection:
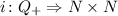
By Cartesian Product of Natural Numbers with Itself is Countable, N×N is countable.
Hence Q+ is countable, by Domain of Injection to Countable Set is Countable.
Note that the function defined by is a bijection. Therefore the composition is a bijection. So the given set is countably infinite.