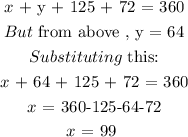Answer:
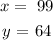
Step-by-step explanation:
Here, we want to get the value of x and y
From the given image, the angle y and 116 lie on a straight line
The sum of the angles on a straight line is 180 degrees
Thus:
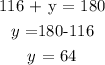
The sum of the internal angles of a polygon can be calculated by the formula:
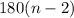
where n is the number of sides the polygon has
In the case of the given question, n is 4
Substituting the value of n, we have it that:
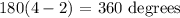
To get the value of x: