ANSWER
a(t) = 18 m/s^2
Step-by-step explanation
We are given that:
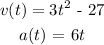
b) To find the acceleration when velocity is 0, we have to find the time at which the velocity is 0.
After finding that, we then find the value of a(t) at that time.
To find the time when velocity is 0, we make v(t) = 0 and find t.
That is:
![\begin{gathered} 0=3t^2\text{ - 27} \\ \Rightarrow3t^2\text{ = 27} \\ \text{Divide through by 3:} \\ t^2\text{ = }(27)/(3) \\ t^2\text{ = 9} \\ t\text{ = }\sqrt[]{9} \\ t\text{ = 3 seconds} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9gpv727sk0ny59u6vr18fa13nt8ikc7aun.png)
Now, we find the value of a(t) when t = 3:
a(t) = 6 * (3)
a(t) = 18 m/s^2
That is the answer.