ANSWER
4/9
EXPLANATION
The probability of not drawing a B in each event is the same because the card is being replaced and the total number of cards is always the same. This probability is equivalent to 1 minus the probability of drawing a B,
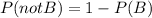
There are 6 cards in total, and 2 of them are B. Thus, the probability of not drawing a B in each event is,
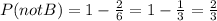
The probability we want to find is the probability of not drawing a B twice in a row,

Hence, the probability of not drawing a B, then not drawing a B is 4/9.