To find the slopes of the line that passes through the points (1, 1) and (7, 5), we can follow the next steps:
1. Identify the coordinates of the points:
x1 = 1
y1 = 1
x2 = 7
y2 = 5
2. Apply the formula of the slope of a line:
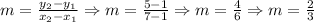
Then, the slope of the line that passes through the points (1, 1) and (7, 5) is m = 2/3.
2. We can follow the same for case 2. (1, 1) and (5, 7):
x1 = 1
y1 = 1
x2 = 5
y2 = 7
Then
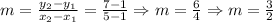
Then, the slope of the line that passes through the points (1, 1) and (5, 7) is m = 3/2.
3. We can follow the same for case 3, (2, 5) and (-1, 2):
x1 = 2
y1 = 5
x2 = -1
y2 = 2
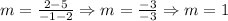
Then, the slope of the line that passes through the points (2, 5) and (-1, 2) is m = 1.
4. We can follow the same for case 4, (2,5) and (-7, -4):
x1 = 2
y1 = 5
x2 = -7
y2 = -4

Then, the slope of the line that passes through the points (2, 5) and (-7, -4) is m = 1.