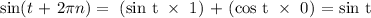Answer:
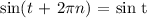
Step-by-step explanation:
Here, we want to use identity to prove a given identity
Using the identity, we have it that:
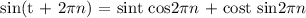
We have it that cos 2pi equals 1 and sin 2pi equals zero
for n integer value that n might be, the product sin 2pi n will evaluate to zero and the product cos 2pi n will evaluate to zero
Thus, we have the evaluation as: