Question

Can you help me or teach me how to do it?

Answer 1

We have an augmented matrix representing a system of equations.

As it has 4 columns and tow rows, we can see that the system has 3 variables (the last column is for the independent term) and 2 equations.

Then, it will have at least one degree of freedom: the value of all the variables will depend on the value of one of the variables.

We can translate the matrix to equations as:

`\begin{gathered} \begin{cases}0x_1+1x_2-6x_3=4 \\ 1x_1-2x_2+10x_3={-2}\end{cases} \\ \\ \begin{cases}x_2-6x_3=4 \\ x_1-2x_2+10x_3={-2}\end{cases} \end{gathered}`

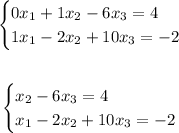
NOTE: we can solve it using row operations but it is easier to understand in this in equation form rather than matrix form.

We can use the first equation to write x2 in function of x3:

`\begin{gathered} x_2-6x_3=4 \\ x_2=6x_3+4 \end{gathered}`

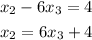
We can now replace x2 in the second equation and then write x1 in function of x3:

`\begin{gathered} x_1-2x_2+10x_3=-2 \\ x_1-2(6x_3+4)+10x_3=-2 \\ x_1-12x_3-8+10x_3=-2 \\ x_1-2x_3=-2+8 \\ x_1-2x_3=6 \\ x_1=2x_3+6 \end{gathered}`

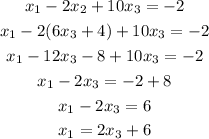
We now see that we have two variables in function of the third one.

If we give x3 a value, then we can find the values of x1 and x2 that satisfy the equations for the value of x3 given.

Answer:

x1 = 2x3 + 6

x2 = 6x3 + 4

x3 is free

[Option A]