Question

Are y=7/3x+6 and y=-3/7x+4 lines parallel perpendicular or neither?I just need a brief explanation with the answer

Answer 1

Step 1: Theorem

Two lines are perpendicular if the product of their slope is equal to -1.

Two lines are parallel if their slope is equal.

Step 2:

`\begin{gathered} \text{Write the general equation of a line in slope-intercept form} \\ y\text{ = mx + c} \\ \text{m = slope} \end{gathered}`

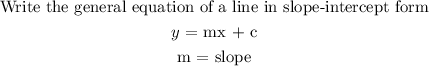
Step 3:

Determine the slope from each equation

`\begin{gathered} y\text{ = }(7)/(3)\text{ x + 6} \\ m_1\text{ = }(7)/(3) \\ y\text{ = }(-3)/(7)x\text{ + 4} \\ m_2\text{ = }(-3)/(7) \end{gathered}`

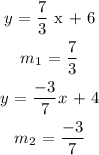
Step 4: Determine if the two lines are parallel or perpendicular.

`\begin{gathered} m_1\text{ }\\e m_2\text{ hence the lines are not parallel} \\ m_1\text{ }* m_2\text{ = }(7)/(3)\text{ }*\text{ }(-3)/(7)\text{ = }(-27)/(27)\text{ = -1} \end{gathered}`

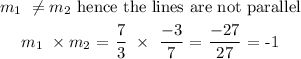
Final answer

Since the product of the two lines is equal to -1, hence, the two lines are perpendicular.

Perpendicular