Step-by-step explanation
We are required to determine the correlation coefficient (r) of the data provided. This should be calculated with the formula:
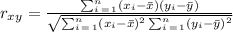
The information can be represented in a table as:
From the table, we have:
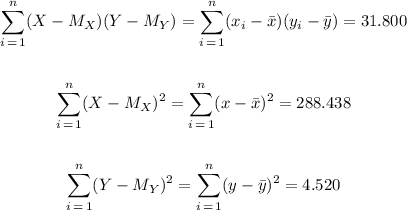
Therefore, we can calculate the correlation coefficient as:
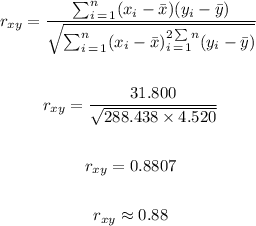
Hence, the answer is 0.88.