5)
5.1
Given equation is
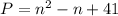
Replace n=1, we get
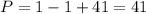
We know that a number divisible by one and itself is called a prime number.
Here 41 is divisible by 1 and 41 only.
Hence 41 is a prime number.
5.2.
Substitute n=37 in the equation of P, we get
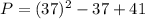
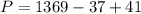
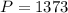
The number 1373 is divisible by one and 1373 only.
So 1373 is a prime number.
Hence if n=37, then P is a prime number.
5.3.
We need to choose three numbers greater than 38.
Let n=39 and substitute in P, we get
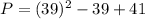
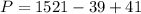
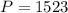
The number 1523 is divisible by one and 1523.
Hence 1523 is a prime number.
Let n=40 and substitute in P, we get
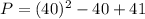
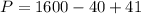
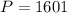
The number 1601 is divisible by one and 1601.
Hence 1601 is a prime number.
Let n=41 and substitute in P, we get
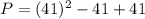
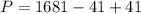
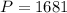
The number 1681 is divisible by one and 1681.
Hence 1681 is a prime number.
We get that
When n=39,40 and 41 then P is prime.
5.4)
Yes, I believe that this conjecture is true.
we have chosen n=1, n=39 0dd number, n=40 even number, and n=41 prime number then we get the prime number for P.
So this conjectures is true for any value of n.
The equation P gives the prime number.