Question

A glass blower can form 8 simple vases or 2 elaborate vases in an hour. In a work shift of no more than 8 hours, the worker must form at least 40 vases.

a. Let s represent the hours forming simple vases and e the hours forming elaborate vases. Write a system of inequalities involving the time spent on each type of vase.
b. If the glass blower makes a profit of $30 per hour worked on the simple vases and $35 per hour worked on the elaborate vases, write a function for the total profit on the vases.
c. Find the number of hours the worker should spend on each type of vase to maximize profit. What is that profit?

Answer 1

`\textsf{a)} \quad \begin{cases}s+e \leq 8\\8s+2e \geq 40\end{cases}`

`\textsf{b)} \quad y = 30s + 35e`

c) 4 simple vases and 4 elaborate vases maximize profit.

The maximum profit is $260.

Explanation:

Given information:

• A glass blower can form 8 simple vases or 2 elaborate vases in an hour.
• In a work shift of no more than 8 hours, the worker must form at least 40 vases.

Part (a)

Define the variables:

• Let s = the number of hours forming simple vases.
• Let e = the number of hours forming elaborate vases.

Create a system of inequalities using the given information and defined variables:

`\begin{cases}s+e \leq 8\\8s+2e \geq 40\end{cases}`

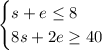
Part (b)

Given information:

• $30 = profit per hour for the simple vases.
• $35 = profit per hour for the elaborate vases.

Let y be the total profit in dollars:

`y = 30s + 35e`

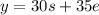
Part (c)

`\begin{cases}s+e \leq 8\\8s+2e \geq 40\end{cases}`

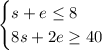
To find the number of hours the worker should spend on each type of vase to maximize profit, find the point of intersection of the two equations.

Isolate e in the first equation:

`\implies e\leq8-s`

Isolate e in the second equation:

`\implies 2e \geq 40-8s`

`\implies e \geq 20-4s`

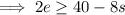
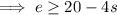
Equate the two expressions for e and solve for s:

`\implies 8-s=20-4s`

`\implies 3s=12`

`\implies s=4`

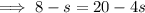
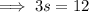
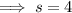
Therefore, the number of hours the worker should spend on each type of vase to maximize profit is:

• Simple vases = 4 hours.
• Elaborate vases = 4 hours.

Substitute the values of s and e into the function from part (b):

`\implies y=30(4)+35(4)`

`\implies y=120+140`

`\implies y=260`

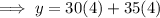
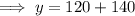
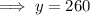
Therefore, the maximum profit is $260.