The point-slope form
The point-slope form is defined as:
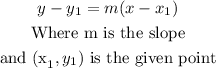
Given:
Slope = 3
point : (6, 2)
Substituting the given value into the given formula:
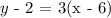
Point-slope form:
y - 2 = 3(x - 6)
Slope-intercept form
The slope intercept form is defined as:
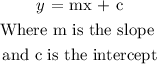
Simplifying the point-slope form, we get the slope-intercept form:
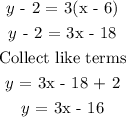
slope-intercept form:
y = 3x - 16