The given graph is a downward parabola.
The roots of the equation is -2 and -8, and the vertex is (-5,7).
The general root form of parabola will be,
a(x-(-2))(x-(-8))=a(x+2)(x+8).
The value of a can be determined from the coordinate of vertex,
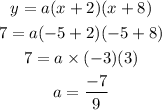
Thus, the required quadratic is,
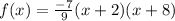
The value of f(-6) can be determined as,
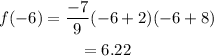
Thus, the requried value of f(-6) is 6.22.